Deterministic Finite Automata in C

In our a5p2 question, we need to write a general template for the deterministic finite automata, with input details are listed below:

If you have the basic concept of what DFA is, let’s then get started. Firstly, we have to understand that DFA is a model or a template for a specific string processing “machine”, thus we do not change the code to adjust the needs for a specific programme, we change the matrix (the $\delta$ ) aka transition table that allows the DFA to determine its validity.

So, firstly, we need to scan in the necessary data listed at the top of this article. Allow me to take Jim’s example with notation aside.

Example 1

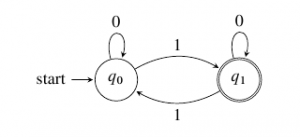
Here is a visualized graph on DFA for determining odd number of 1’s in a binary input. As long as the 1’s are odd, the input is accepted.

Graphed like this:

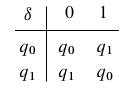
The transition table is correspondingly this:

2 //the number of states ( $q_0, q_1, ..., q_{n-1}$ )
1 //the number of final states, we have only 1 final state here.
2 //the number of final symbols in $\Sigma$
1 //the final state is $q_1$ . If DFA ends here, then the input is valid.
01 //the valid characters in symbols.
0 1
1 0 //those 2 lines are the transition table, meaning $q_0 q_1$ and $q_1 q_0$ .

Let’s give out an input stream sample: 010000011

The initial state is $q_0$ . 0 goes in, it looks for coordinate $(0, q_0)$ , the result is still $q_0$ .

Current state is $q_0$ , then 1 goes in, it looks for $(1, q_0)$ . State is changed to $q_1$ .

Then five 0s goes in, the state is locked to $q_1$ based on what the transition table says.

Then 1 goes in, state is now $q_0$ .

Finally the last 1 is passed in, state is changed to $q_1$ .

EOF

The DFA stopped with a state at $q_1$ , because only $n \in |F|$ is valid, in this case, $q_1$ is valid, so the input is valid.

Example 2

The visual graph is like this:

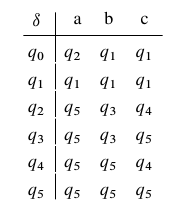
and the transition table is like this:

The input for building DFA will be like this:

6
3
3
2 3 4
abc
2 1 1
1 1 1
5 3 4
5 3 5
5 5 4
5 5 5

Similarly, there are 6 states, from 0~5. 3 final states, they are $q_2 q_3 q_4$ . There are 3 characters accepted, which are $a, b, c \in \Sigma$ , and the matrix map.

How to write this programme?

Well firstly we need to read the data in and build a matrix. Then we need to move around the matrix table and get its state, and finally compare the state to the final states.

The code is relatively simple:

#include 
#include 
#include 

#define N_ASCII 256
#define ACCEPT 200

int
dfa(int nstate, int nfinal, int nsymbol)
{
    int i, j, c, state = 0;
    int final[nfinal];
    int symbol[N_ASCII] = {0}, acceptable_chars[N_ASCII] = {0};
    int matrix[nstate][nsymbol];
    
    /* Buidling up the DFA */

    /* Scanning the final states */
    for (i = 0; i < nfinal; i++)
    {
        scanf("%d", &final[i]);
    }
    scanf("%*[*^\n]\n");

    /*
     * Scan in the chars that are accepted by DFA, allocate its tag from 0 to
     * 1 in symbol[c].
     */
    for (i = 0; i < nsymbol; i++)
    {
        c = getchar();
        symbol[c] = i;
        acceptable_chars[c] = ACCEPT;
    }
    scanf("%*[*^\n]\n");

    /* Scan in the \delta transition table */
    for (i = 0; i < nstate; i++)
    {
        for (j = 0; j < nsymbol; j++)
        {
            scanf("%d", &matrix[i][j]);
        }
    }
    scanf("%*[*^\n]\n");

    /* 
     * Test the input steam
     * We'll stop at either EOF or \n
     */
    bool empty = true;
    while ((c = getchar()) != EOF && c != '\n')
    {
        if (!(acceptable_chars[c] == ACCEPT))
        {
            fprintf(stderr, "/%c/ char is not in the symbol list!\n" 
                    "Because your number of symbols is %d " 
                    "and there is a %dth.\n", c, nsymbol, nsymbol + 1);
            return -1;
        }

        /* 
         * Inside the matrix we move around based on the char's nth number,
         * until the last getchar().
         */
        state = matrix[state][symbol[c]];
        empty = false;
    }

    if (empty == true)
    {
        fprintf(stderr, "No test input detected!\n");
        return -1;
    }

    for (i = 0; i < nfinal; i++)
    {
        /* 
         * Then we check the final state, if it's a match with any of the 
         * elements inside of |F|
         */
        if(state == final[i])
        {
            return 1;
        }
    }

    return 0;
}

int
main(int argc, char *argv[])
{
    int nstate, nfinal, nsymbol, ret;
    ret = scanf("%d\n", &nstate);
    if (ret != 1)
    {
        fprintf(stderr, "No. of states is invalid!\n");
        return EXIT_FAILURE;
    }
    ret = scanf("%d\n", &nfinal);
    if (ret != 1)
    {
        fprintf(stderr, "No. of finals is invalid!\n");
        return EXIT_FAILURE;
    }
    ret = scanf("%d\n", &nsymbol);
    if (ret != 1)
    {
        fprintf(stderr, "No. of symbols is invalid!\n");
        return EXIT_FAILURE;
    }
    ret = dfa(nstate, nfinal, nsymbol);

    if (ret == 0)
    {
        printf("Not accepted.\n");
    }
    else if (ret == -1)
    {
        fprintf(stderr, "Invalid input.\n");
        return EXIT_FAILURE;
    }
    else
        printf("Accepted.\n");

    return EXIT_SUCCESS;
}

This has to be compiled using -std=c99 flag in gcc.

When I wrote this program, I did not consider '\n' as a valid element of set $\Sigma$ .

Deterministic Finite Automata in C

Example 1

Example 2

Related

Leave a comment

Leave a Reply Cancel reply